もともと、このアルゴリズムは、私のアイディアで考案し、発表したものの、
すでに、in-place merge ソートというアルゴリズムの考え方に、非常に似ていることが判明しました。
また、計算量がO(N^2)であることが推定され、特に、速い部類には入らないことも判明しました。
このまま、わかりずらいアルゴリズムの紹介のみで終わらせてしまうと、このソートに興味を示された方々に、
申し訳ないので、ここに、ソースコード(下記に示すパフォーマンステストのソース)を公開することにしました。
replaceperformancetest.zip
一昔前のPC(CPU)では、力を発揮する可能性はありますが、最近のPCでは、挿入ソートより遅いです。
その点だけ注意してください。
データの中央を基準値にします。
左右のデータを、基準値と比較していきます。
9,11,8,12,7,13・・・
左… 基準値より大きいデータがあれば、右に寄せます。
右… 基準値より小さいデータがあれば、左に寄せます。
データの移動先にあるデータの順番が狂わないように順次、左右に寄せます（安定ソートを維持するため）
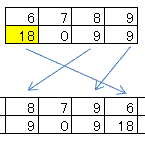
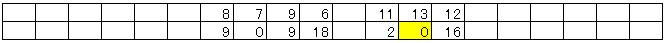
以上を、左右の端に行きつくまで繰り返します。
左… 基準値より大きいデータが右に、小さいデータは左に寄ります。
右…
基準値より小さいデータが左に、大きいデータは右に寄ります。
左側の大きいデータ群と、右の小さいデータ群を入れ替えます(replace)。
基準値より小さいデータ群、大きいデータ群とに分けて再帰的に並べ替えをします。
Pentium4
1.8GHzの結果 |
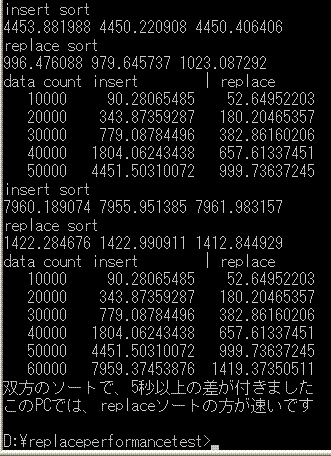
Pentium4 HT 3.0GHzの結果 ※使い古しのWindows上での結果ですので、安定していませんん。あくまで、参考値  |
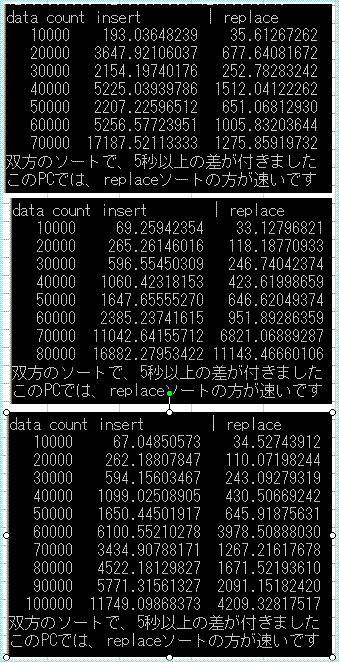少なくとも、Pentium4系列のCPUでは、挿入ソートより、半分以下の時間で、ソートが完了する結果となりました。
安定ソートの選択肢として、insert(挿入)ソートは、あり得ません。
なお、以下は、知り合いに、協力して頂いた結果です。
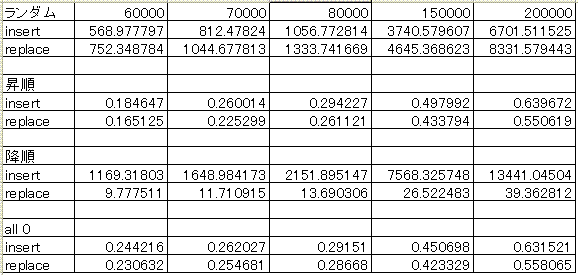
| Core i7 上段は、データ数です。 小数点込みで記述されているのは、時間(ms) さすがに、最新のCPUでは、insert(挿入ソート)の方が、若干いい結果を残しています。 ただ、降順の並びを昇順に並び返す場合は、挿入ソートの比ではありません。  |